FUZZY LOGIC (LOGIKA FUZZY)

Jadi Logika Fuzzy digunakan untuk :
1.Fuzzy Logic suatu teknik yang digunakan untuk menangani ketidakpastian masalah-masalah yang memiliki banyak jawaban.
2. Untuk merepresentasikan masalah yang mengandung ketidakpastian ke dalam suatu bahasa formal yang dipahami komputer.
Contoh Aplikasi Logika fuzzy :
1. Pengontrol kereta bawah tanah disendai, Jepang.
2. Pengatur mekanisme otofocus pada kamera
3. Sistem pengeraman mobil (nissan)
4. Penghematan konsumsi daya listrik pada AC
5. Otomatisasi kecepatan putar mesin cuci terhadap tebal-tipis atau banyak-sedikit jenis pakaian dalam mesin cuci
6. Penentuan prestasi mahasiswa berdasarkan great IPK
7. Kontrol jumlah produksi barang berdasarkan permintaan konsumen
8. Penentuan karyawan terbaik berdasarkan indeks kinerja
9. Kontrol kecepatan kendaraan berdasarkan cuaca terkini
Konsep dan Pengertian fuzzy logic :
– Fuzzy adalah sebuah cara memetakan ruang-input ke dalam ruang output
– Fuzzy pada dasarnya sudah terbawa sejak lahir, seperti pertanyaan tentang “seberapa besar ?, seberapa kecil?, secepat apa ? dll”.
– Yang terpenting adalah “The way of thinking-Terhadap Permasalahan” di lingkungan sekitar.
Contoh-Contoh problem yang dapat dipetakan dengan fuzzy:
1. Manager-gudang mengatakan kepada manager produksi “kita telah mendapat pesanan lebih besar dalam minggu ini. Tolong dicekkan, berapa banyak jumlah persediaan kita di gudang. Dan berapa besara barang yang harus akan diproduksi”.
2. Seseorang mengatakan kepada kita “Seberapa sejuk ruangan yang saudara inginkan ? Saya akan mengatur putaran kipas dalam ruang ini.
3. Bilaseseorangmengatakan “Jikasaatinicuacanyacerahdanpanas, sayaakanmengemudidengancepat“
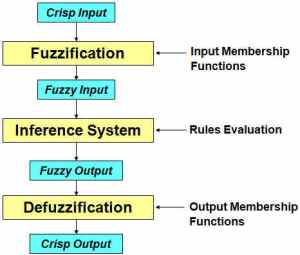
Arsitektur Logika Fuzzy :

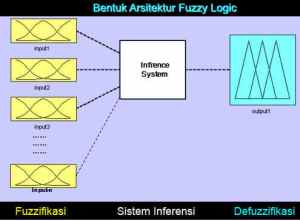
1. Fuzzifikasi, Proses konversi input-input (masukan) yang bersifat tegas (crips) ke dalam bentuk (fuzzy) variabel linguistik menggunakan fungsi keanggotaan
2. Sistem Inferensi, Proses pengkonversian input-fuzzy menggunakan aturan-aturan “If-Then” menjadi Output-Fuzzy
3. Defuzzifikasi, Proses konversi Output-Fuzzy dari sistem inferensi ke dalam bentuk tegas (crips) menggunakan fungsi keanggotaan serupa (sebelumnya) menjadi sebuah nilai

Jadi dari sisi flow chart pemrosesan, struktur fuzzy dapat dilihat dalam flow di bawah :

Hal Dasar Dalam Logika fuzzy :
A. Himpunan Tegas (Crisp Set)
– Himpunan yang membedakan anggota dan non anggotanya dengan batasan yang jelas disebut crisp set.
– Misalnya, jika C={x | x integer, x > 2}, maka anggota C adalah 3, 4, 5, dan seterusnya.
– Sedangkan yang bukan anggota C adalah 2, 1, 0, -1, dan seterusnya

B. Himpunan Fuzzy (Fuzzy Set)
– Fuzzy set merupakan dasar dari fuzzy logic dan fuzzy systems.
– Suatu fuzzy set A di dalam Universe (semesta) U didefinisikan sebagai suatu fungsi keanggotaan u-A[x] (sebut miu A), yang memetakan setiap objek di U menjadi suatu nilai real dalam interval [0,1].
– Nilai-nilai u-A[x] menyatakan derajat keanggotaan x di dalam A.

Contoh Himpunan Tegas dapat dilihat pada sebagai berikut :
1. Misalkan, x = {5, 10, 20, 30, 40, 50, 60, 70, 80} adalah crisp set Usia dalam satuan tahun.
2. Balita, Dewasa, Muda, dan Tua adalah empat fuzzy set yang merupakan subset dari x
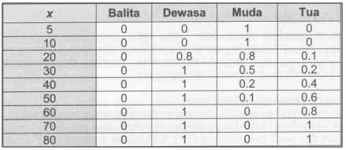Pada tabel di atas, terdapat 4 buah fuzzy set dengan anggota dan derajat keanggotaannya sebagai berikut :
– Balita = {}.
– Dewasa = {20, 30, 40, 50, 60, 70, 80}, di mana derajat keanggotaannya dinyatakan oleh u-Dewasa = {0.8, 1, 1, 1, 1, 1, 1}.
– Muda = {5, 10, 20, 30, 40, 50}, di mana derajat keanggotaannya dinyatakan oleh u-muda = {1, 1, 0.8, 0.5, 0.2, 0.1}
– Tua = {20, 30, 40, 50, 60, 70, 80}, di mana derajat keanggotaannya dinyatakan oleh u-Tua = {0.1, 0.2, 0.4, 0.6, 0.8, 1, 1}

C. Fungsi Keanggotaan (Membership Function)
– Di dalam fuzzy sistems, fungsi keangotaan memainkan peranan yang sangat penting untuk merepresentasikan masalah dan menghasilkan keputusan yang akurat.
– Terdapat banyak sekali fungsi keanggotaan yang bisa digunakan, Tetapi disini akan dibahas 4 fungsi keanggotaan, yaitu

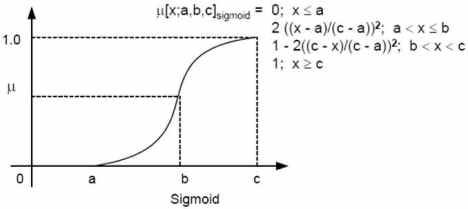
1. Fungsi Sigmoid, fungsi dan bentuknya seperti pada gambar di bawah :
– Sesuai dengan namanya, fungsi ini berbentuk kurva sigmoidal seperti huruf S.
– Setiap nilai x (anggota crisp set) dipetakan ke dalam interval [0,1].

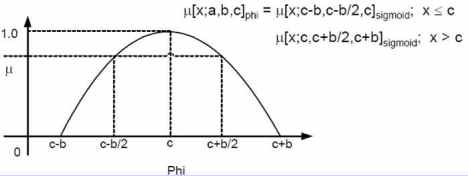
2. Fungsi Phi
– Pada fungsi keanggotaan ini, hanya terdapat satu nilai x yang memiliki derajat keanggotaan yang sama dengan 1, yaitu ketika x=c.
– Nilai-nilai di sekitar c memiliki derajat keanggotaan yang masih mendekati 1

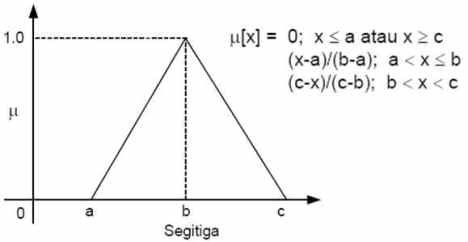
3. Fungsi Segitiga
– Sama seperti fungsi phi, pada fungsi ini juga terdapat hanya satu nilai x yang memiliki derajat keanggotaan sama dengan 1, yaitu ketika x=b.
– Tetapi, nilai-nilai di sekitar b memiliki derajat keanggotaan yang turun cukup tajam menjauhi 1

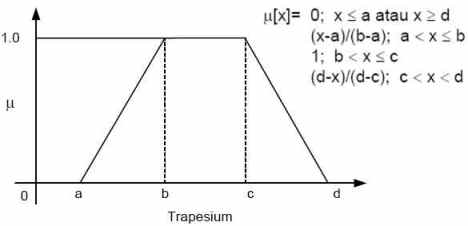
4. Fungsi Trapesium
– Berbeda dengan fungsi segitiga, pada fungsi ini terdapat beberapa nilai x yang memiliki derajat keanggotaan sama dengan 1, yaitu ketika b ≤ x ≤ c.
– Tetapi derajat keanggotaan untuk a < x < b dan c < x ≤ d memiliki karakteristik yang sama dengan fungsi segitiga

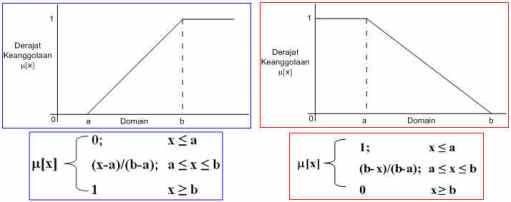
5. Fungsi Linier (naik & turun)
Bentuk ini adalah bentuk paling sederhana dan menjadi pilihan yang baik untuk mendekati konsep yang kurang jelas. Representasi fungsi ini ada 2 macam, linier naik dan linier turun

6. Fungsi Kurva Bentuk Bahu
– Fungsi pada dasarnya adalah gabungan antara fungsi segitiga dan fungsi linier.
– Kurva bentuk bahu sering digunakan dalam penyelesaian permasalahan fuzzy, baik yang model linier maupun model sigmoid

CONTOH KASUS Dan PENYELESAIANNYA

Kita ambilkembalikesalahsatupermasalahansebelumnya, yaitu Bila seseorang mengatakan “Jika saat ini cuacanya cerah dan panas, saya akan mengemudi dengan cepat“.
Bila kita perhatikan permasalahan dalam kalimat di atas, MAKA :
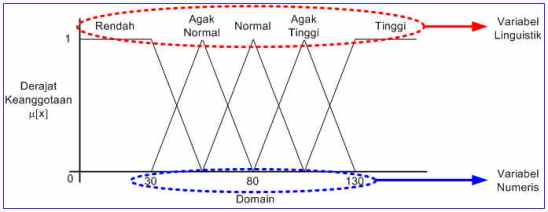
Variabel linguistik fuzzy, digunakan untuk merepresentasikan kualitas jangkauan yang lebih spesifik sebagaimana berikut:
1. Temperatur (dingin, sejuk, hangat, panas)
2. Keadaan awan (mendung, agak mendung, cerah)
3. Kecepatan (slow, fast).
TETAPI, Pertanyaannya :
Pertanyaan : “Bagaimana kondisi suhunya ?”
Jawaban : “Sekarang Hangat / Agak Panas”.
Pertanyaan : “Bagimana Maksud “Hangat”-nya itu ?”
PROSES FUZZIFIKASI
Nah, Beirkutnya kita harus mengkonversi variabel lingusitik temperatur/suhu diatas menjad tabel dengan menggunakan fungsi kurva bahu seperti di bawah ini.

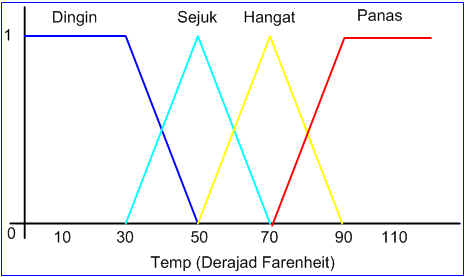
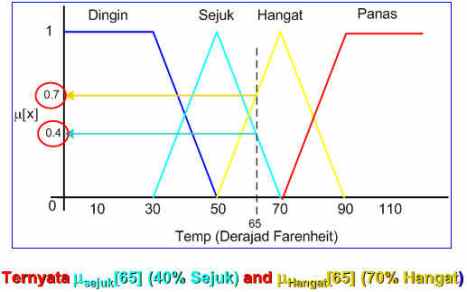
kemudian kita buat permisalan bahwa suhu sekarang yang terbaca oleh sensor suhu adalah = 65 derajad.

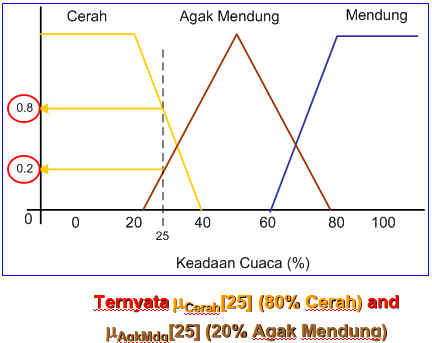
Selanjutnya adalah kita harus mengkonversi variabel lingusitik keadaan awan diatas menjadi tabel dengan menggunakan fungsi kurva bahu seperti di bawah ini.

Lalu kita buat permisalan bahwa keadaan awan sekarang yang terbaca oleh sensor adalah = 25%.

JADI, Proses Fuzzifikasi telah menghasilkan 4 input_fuzzy, yaitu :

PROSES SISTEM INFERENSI
– Sistem inferensi adalah pemrosesan input-fuzzy menjadi output-fuzzy melalui aturan-aturan (rules).
– Terdapat berbagai cara untuk menentukan aturan fuzzy.
– Misalkan output-fuzzy dipetakan bentuk fungsi keanggotan kecepatan seperti di bawah
Dalam kasus ini, variabel yang mempengaruhi output hanya terdapat 2 variabel saja, Sehingga Matrik_Relasi_Fuzzy yang digunakan untuk menggernerate rule-rule fuzzy berdimensi 2 (D2), sepertri pada gambar di bawah.

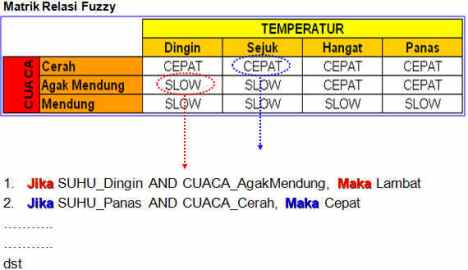
Dari tabel dimensi 2 diatas, akan harus dibuat keputusan tentang relasi antara atribut variabel_lingusitik_temperatr dengan variabel_lingusitik_cuaca dalam bentuk kecepatan (Cepat atau Sedang, atau Lambat). Nah, tentu saja keputusan “cepat atau lambat” dalam hal ini seharusnya adalah berdasrkan kebijakan lokal atau berdasarkan hasil penelitian.
Jadi hasil secara kesuluruhan rule-rule berdasarakn tabel berdimensi 2 diatas adalah sebagai berikut :


PROSES DEFUZZYFIKASI

Sumber : https://yusronrijal.wordpress.com/2012/03/27/logika-fuzzy/